跳转至

Boyer-Moore 算法

给定文本字符串 \(txt[0,n-1]\)（以下称为 \(T\)） 和模式字符串 \(pat[0,m-1]\)（以下称为 \(P\)），在 \(T\) 中查找 \(P\)（假定 \(n\ge m\ge 1\)）。

算法

BM 算法从右往左进行比较匹配，与 KMP 算法相似，BM 算法通过预处理模式串，使得匹配失败时，模式串可以向后移动多位，即利用模式串的一些特征，排除无法匹配的的位置，加快了匹配的速度。

BM 算法包含两个启发策略来移动模式串：坏字符规则 和 好后缀规则。

坏字符规则

当从右往左，出现匹配失败时，

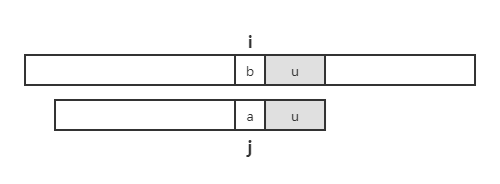
mismatch.png

我们称 b 为 坏字符，即不匹配的字符，此时分两种情况讨论：

如果模式串 \(P\) 包含 b，将最右侧的 b 和坏字符对齐（若 b 在 a 右侧，则右移一位）；

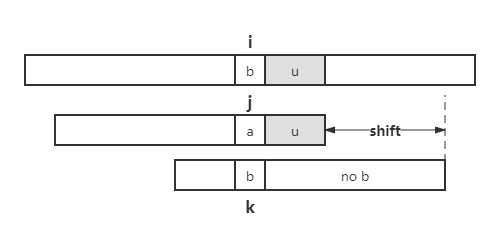
contained.png

\[ \begin{equation} shift(\text{'b'})=\max\{1,\ j+1-k\},\ k=\text{lastIndexOf('b') } \end{equation} \]

如果模式串 \(P\) 在 a 的左侧不包含 b，则将整个模式串移至坏字符右侧。

not contained.png

\[ \begin{equation} shift(\text{'b'})=j+1 \end{equation} \]
class BM {
    // 如果字符集较小，可以用数组代替
    Map<Character, Integer> badChar(char[] pat) {
        Map<Character, Integer> lastIndices = new HashMap<>();
        for (int i = 0; i < pat.length; i++) {
            lastIndices.put(pat[i], i);
        }
        return lastIndices;
    }
}

好后缀规则

当从右往左，出现匹配失败时，

mismatch.png

我们称已经匹配的部分 u 为 好后缀，此时分三种情况讨论：

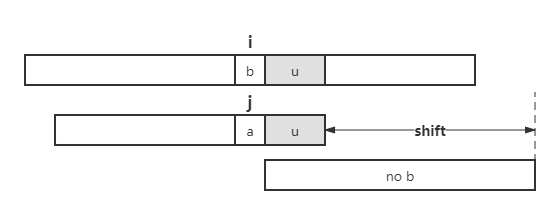
如果模式串 \(P\) 在 a 的左侧包含 u，将其中最右侧的 u 与好后缀对齐；

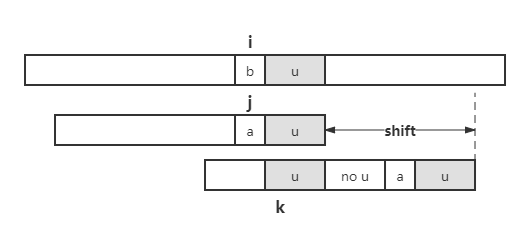
contained.png

\[ \begin{equation} shift(j)=j+2-k,\ k=\text{lastIndexOf(u,0,j+1) } \end{equation} \]

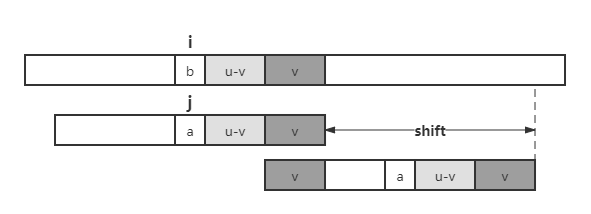
如果模式串 \(P\) 在 a 的左侧不存在完全匹配的 u，但是存在最长的子串 v 既是 u 的后缀，也是 \(P\) 的前缀，则将二者对齐；

suffix.png

\[ \begin{equation} shift(j)=m-k,\ k=\text{the length of the longest common prefix and suffix of }P \end{equation} \]

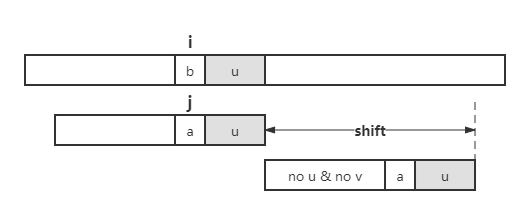
如果上述两步都不满足，则将整个模式串移至好后缀右侧。

no suffix.png

\[ \begin{equation} shift(j)=m \end{equation} \]

优化

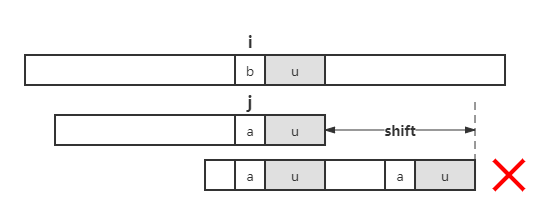
在情况一中，当我们寻找出现在 \(P\) 中的其他 u 时，利用已经失配的字符 a 可以排除一些错误结果，即，如果找到的 u 的前一个字符是 a，则可以忽略。

exclude.png

计算

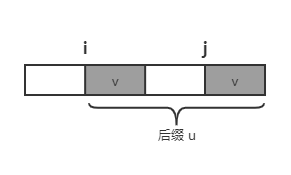
首先计算模式串 \(P\) 每个后缀子串 u（\(P[i,m-1]\)）的最长公共前缀后缀（不包括 u 本身）对应的后缀起始位置 \(j\)，令 \(j=f(i)\)，

preprocess.png

我们从右往左进行归纳，当 \(i=m-1\) 时，\(f(m-1)=m\)，

假设当 \(i=s\) 时，\(f(s)=t\)，

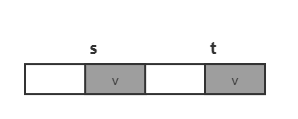
preprocess.png

考虑 \(i=s-1\)，

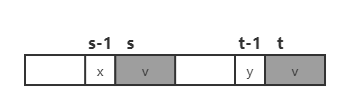
preprocess.png

如果 x=y，则 \(f(s-1)=t-1=f(s)-1\)；

如果 x\(\neq\)y，考虑 \(f(t)\)，

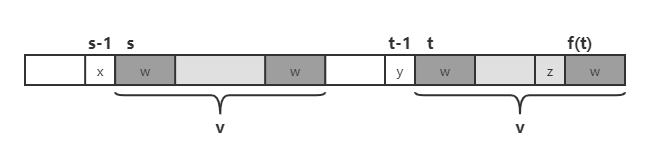
preprocess.png

如果 x=z，则 \(f(s-1)=f(t)-1=f(f(s))-1\)；否则，考虑 \(f(f(t))\)，以此类推。

在整个 BM 算法中，每次匹配失败后，模式串向右移动的距离取两个规则中的较大值。

参考